Camparison of Newmark-beta method and Generalized-alpha method
Recently, I was working on solving some phase-field based fracture problems, where I need to do time marchings to let the fracture propagate in time domain. Taking this opportunity, I reviewed a bunch of numerical methods for ODEs. Different methods have different accuracies and are focused on different type of problems. Although Runge-Kutta method and Backward Euler method are well known to numerical people in their accuracy and stability, in finite element field, people like to use Newmark-$\beta$ method and Generalized-$\alpha$ method. The reason is because these two methods allows to solve second order ODEs directly without introducing any state variables. Hence, I reviewed the performances of of these two methods in detail. In case I forget their properties later on, I’d like to document my study here.
Problem
In general, a dynamic finite element problem can be written as
where $\mathbf{M}$, $\mathbf{C}$, $\mathbf{K}$, are mass, damping and stiffness matrix, respectively. $\mathbf{d}$ is the displacement vector and $\mathbf{f}$ is the external load vector.
Now, the problem is: Given the displacement, speed and acceleration at certain time $(t_n)$, how to find their values at the next time step $(t_{n+1}:=t_n+\delta{t})$. The two methods we are about to discuss are designed to tackle this issue.
Newmark-$\beta$ method
The Newmark-$\beta$ method was proposed in 1959 and is widely used in solve $2^{nd}$ order dynamic problems nowadays. The scheme is given as:
The primary requirement of numerical algorithms is that they should provide adequate good approximations of exact solution. The definition of ‘adequate good’ contains two aspects: stability and accuracy, and the accuracy of a numerical method heavily depends on its stability. From these two properties, we can determine the values of $\gamma$ and $\beta$.
Stability
Stability means, for a given disturbance in the solution for a certain moment, its influence should eventually fades out. To demonstrate this conception, we consider a dampingless singule-degree-of-freedom (SDOF) problem (Indeed, any dampingless system can be decomposed into SDOFs by spectral decomposition.):
Once we have the above expression, we can solve in terms of $\mathbf{X}_{n}$ as
with
where $\Omega=\omega\delta{t}$. The matrix $\mathbf{A}$ is called amplification matrix. The above formulation allows us to do time stepping by matrix multiplications as . The stability requires that all eigenvalues of the amplification matrix should have magnitude that less than 1 so that any disturbance (in terms of $d$, $v$ or $a$) will be completely damped out (at least not be magnified). By solving the characteristic equation of $\mathbf{A}$, we can obtain three eigenvalues. By applying the magnitude constraint on these three eigenvalues, we can deduce the range of $\gamma$, $\beta$ and $\Omega$ (Indeed, what we really care about is the time step size $\delta{t}$.) that we are allowed to choose. You can use any symbolic math tool to solve this problem, the results are
- $2\beta\geq\gamma\geq\frac{1}{2}$ for all $\Omega\geq{}0$. In other words, it is stable for any choice of the time step size $\delta{t}$. This is also called unconditionally stable.
- $\gamma\geq\frac{1}{2}$ && $\beta\leq\frac{\gamma}{2}$ && $\Omega\leq{\frac{2}{\gamma-2\beta}}$. This is also called conditionally stable, because there is an additional constraint on the time step size.
Because of the constraint on $\Omega$, sometimes we need to find the highest frequency $\omega$ in the finite element linear system to identify the largest feasible time step.
Accuracy
A numerical method is accurate if $||u-u^h||\rightarrow{}0$ as $\delta{t}\rightarrow {}0$. However, accurate methods can differ in their efficiency, that is the approximted result can converge to analytical solution in different speeds. In this section, we will discuss the convergence rate of Newmark-$\beta$ in detail.
Since there are three fields ($d$, $v$ and $a$) involved in the original formulation, for the sake of simplification, we should try to eliminate some of them. Here we consider a multi-step system
From the above linear system, we can eliminate all speed and accelerations terms, resulting in a pure displacement equation as
The expression of coefficients $A_i$ are quite clumsy, and the derivation procedure is tedious, but again you can use symbolic math tools to do it very quickly. By replacing numerical solution $d_{n+i}$ with exact solution $d(t_{n+i})$ and doing Taylor expansion on each displacement terms w.r.t $d(t_{n})$, we end up with the truncation error
Hence, in general, Newmark-$\beta$ is a first order accurate method, but if we can let
the first order truncation error can be completely eliminated. As a result, we improve Newmark-$\beta$ to second order accuracy.
Issues
Although Newmark-$\beta$ method had been widely used by FEA/CFD people, it has disadvantages which makes it less attractive and various methods nowadays have been proposed to replace it. The main issue for Newmark method is that there is no way to introduce numerical damping when $\gamma=\frac{1}{2}$. In dynamic problem, high frequency modes normally describe motions with no physical sense (also contains very large phase error), hence, algorithmic damping in the high frequency regime is desired.

However, as demonstrated in the above figure, the spectral radious for $\gamma=\frac{1}{2}$ is $1$ for the entire spectral. By increasing $\gamma$, we observe dissipations in moderate frequency, but still no high frequency damping at all.
Generalized-$\alpha$ method
Generalized-$\alpha$ method is proposed by Chung and Hulbert. Its scheme is
Following the similar paradigm, we now derive the constraints on parameters by considering the stability and accuracy of the algorithm.
Accuracy
By reducing $\mathbf{d}_{n+1-\alpha_f}$, $\mathbf{v}_{n+1-\alpha_f}$ and $\mathbf{a}_{n+1-\alpha_m}$ and disregard the damping term, we can obtain the truncation error
Hence, $\gamma=\frac{1}{2}-\alpha_m+\alpha_f$
Stability
Since too many variables are involved in the amplification matrix $\mathbf{A}$, which will make the stability analysis a impossible mission. Hence, we simplify the problem by considering two extreme situations – zero stable and infinity stable.
Zero stable
Here we consider the stability for $\Omega\rightarrow{0}$.
Three roots of the characterist equation of the above amplification matrix are $\lambda_1^0,\lambda_2^0=1$, $\lambda_3^0=\frac{\alpha _f}{\alpha _f-1}$, which indicates a stability constraint $\alpha _f\leq{\frac{1}{2}}$.
Infinity stable
Here we consider the stability for $\Omega\rightarrow{\infty}$.
Three roots are $\lambda_1^\infty=\frac{\alpha _f}{\alpha _f-1}$, $\lambda_2^\infty,\lambda_3^\infty=\frac{4 \beta -2 \gamma -1\pm\sqrt{(2 \gamma +1)^2-16 \beta }}{4 \beta }$, respectively. If the roots $\lambda_2^\infty,\lambda_3^\infty$ are complex conjugates, we have $\vert\lambda_1\vert\leq{}1$ && $\lambda_2\lambda_3<{1}$ $\rightarrow{\alpha _m<\alpha _f\leq{\frac{1}{2}}}$. If the roots $\lambda_2^\infty,\lambda_3^\infty$ are real numbers, the stability constraints are given by $\gamma >\frac{1}{2}$, $\frac{\gamma }{2}\leq \beta \leq \frac{1}{16} \left(4 \gamma ^2+4 \gamma +1\right)$. As a result, for second order accuracy, the generalized-$\alpha$ method is unconditionally stable, provided
Dissipation
Ideally, a good algorithm should maintain low frequency modes and minimize the effect of high frequency modes. In the stability analysis, we observed that $\lambda_1^0,\lambda_2^0=1$, which means low frequency modes are preserved. How, we take $\lambda^\infty$ as a new design variable for the choice of numerical parameters.
From the original paper, it says ‘High-frequency dissipation is maximized if the principal roots become real in the high-frequency limit (which I don’t quite understand yet.). Hence, we can find
The three roots can be rewritten as: $\lambda_1^\infty=\frac{\alpha _f}{\alpha _f-1}$, $\lambda_2^\infty,\lambda_3^\infty=\frac{\alpha_f-\alpha_m-1}{\alpha_f-\alpha_m+1}$. By requiring $\lambda_1^\infty=\lambda_2^\infty=\lambda_3^\infty=\lambda^\infty$, we find
Now, we look at the spectral radii of Generalized-$\alpha$ method below, it provides more favorable behavior.

A simple example
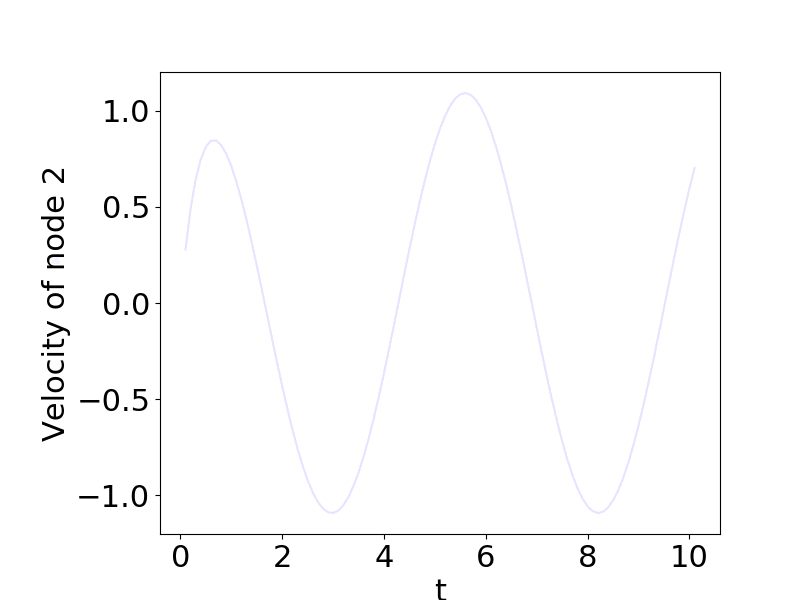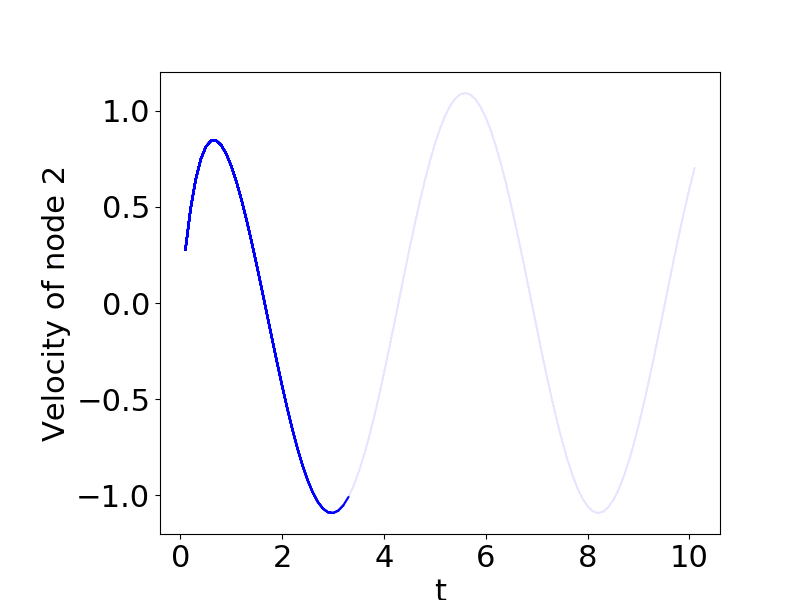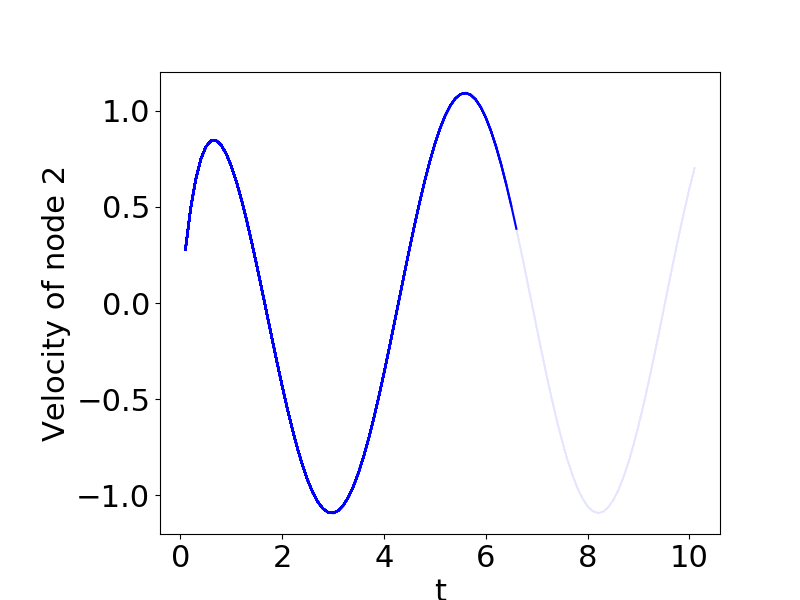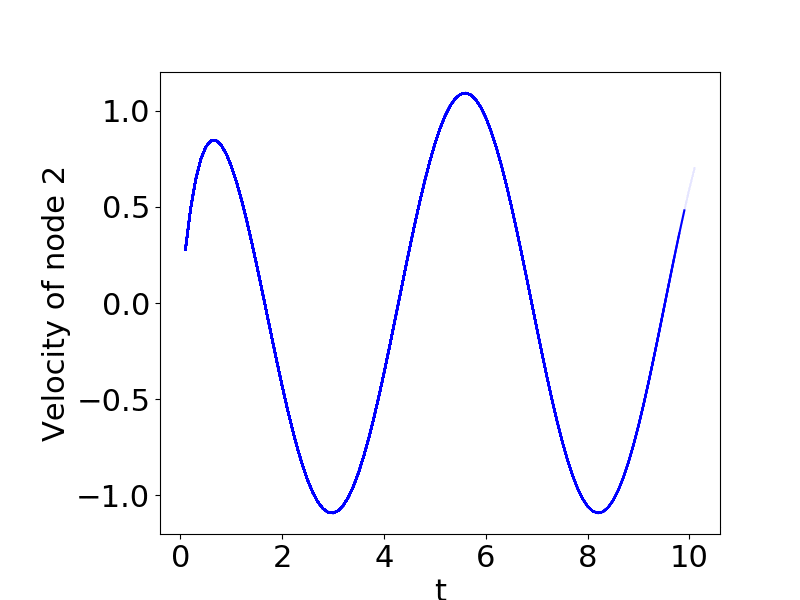
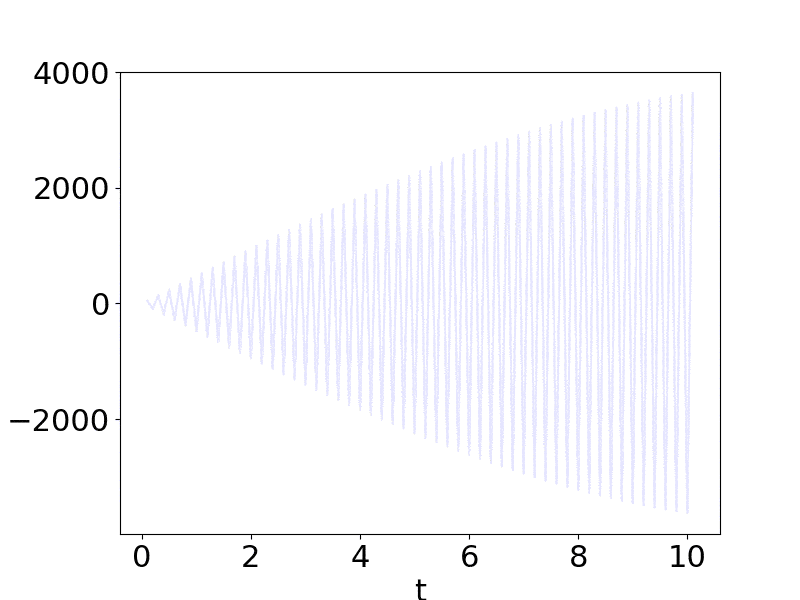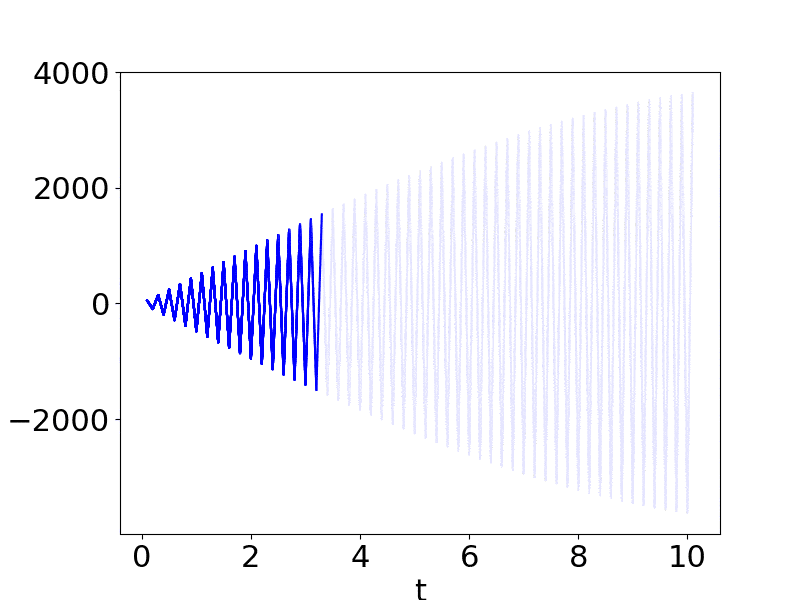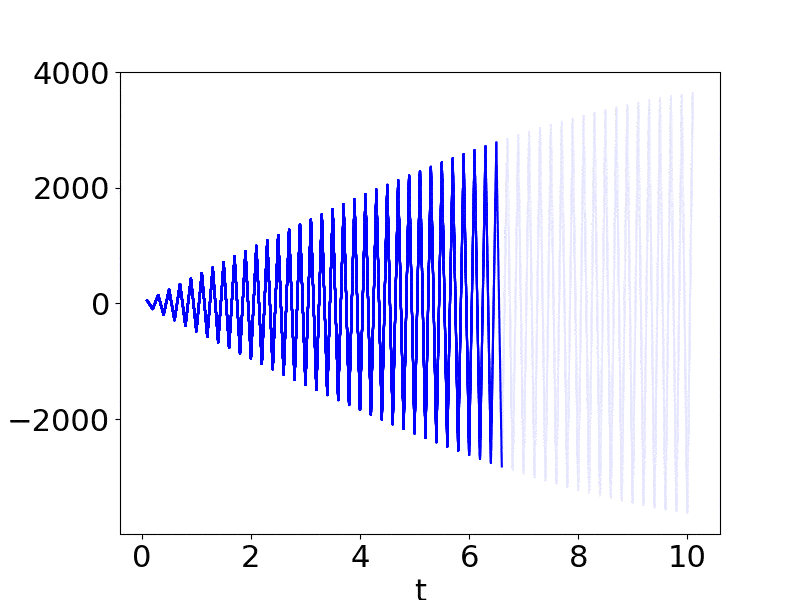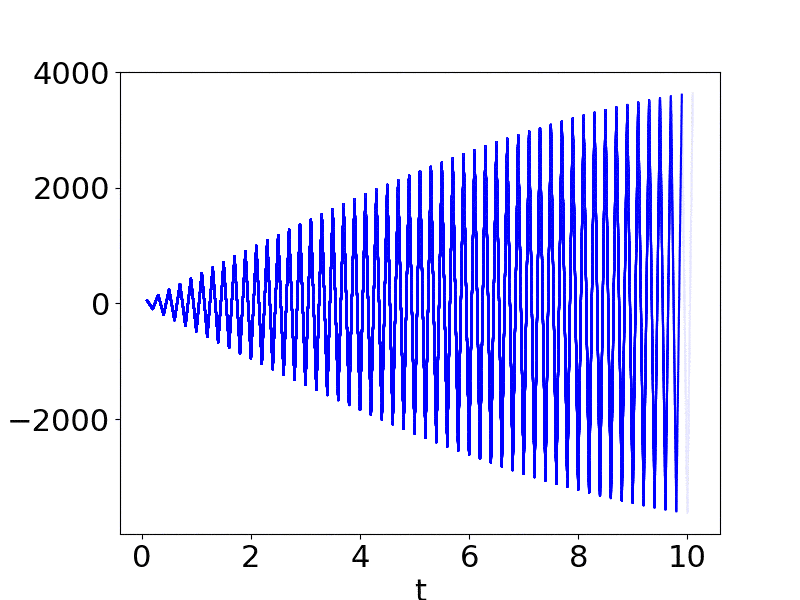
Leave a Comment